728x90
반응형

1735번: 분수 합
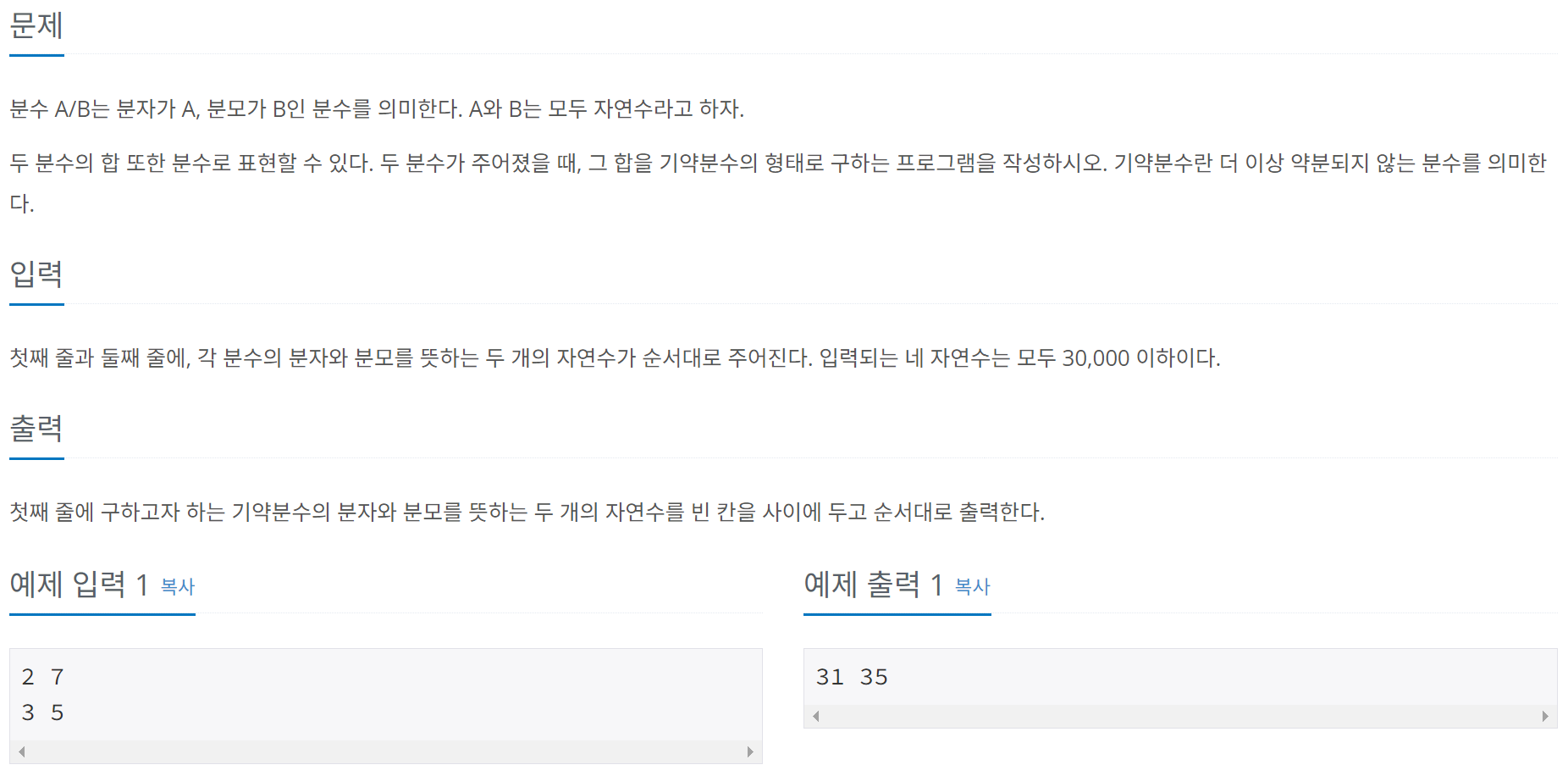
첫째 줄과 둘째 줄에, 각 분수의 분자와 분모를 뜻하는 두 개의 자연수가 순서대로 주어진다. 입력되는 네 자연수는 모두 30,000 이하이다.
www.acmicpc.net
1. 문제 설명
2. 풀이과정
해당 문제는 두 분수를 입력받아 그 합을 구하는 문제이다.
두 분수를 더했을 때, 그 결과를 기약분수로 구해야 한다.
기약분수는 더 이상 약분되지 않는 분수이므로 각 분자와 분모의 최대공약수를 구해 분자와 분모를 이로 나눠야 한다.
최대공약수는 유클리드 호제법을 활용하여 빠르게 구할 수 있는데, 유클리드 호제법이란 두 수를 서로 나누어 최대공약수를 구하는 방법이다.
유클리드 호제법은 "a % b = r이라고 할 때, a와 b의 최대공약수는 b와 r의 최대공약수와 같고, 이를 다시 b % r = r'이라고 할 때, b와 r의 최대 공약수는 r과 r'의 최대공약수와 같다."를 활용하여 나머지가 0이 되었을 때 나누는 수가 원래 두 수의 최대공약수임을 활용하는 방법이다.
- sys.stdin.readline() 함수를 사용하기 위해 sys 모듈을 불러온다. import sys
- 첫 번째 분수의 분자와 분모를 입력받는다. A, B = map(int, sys.stdin.readline().split())
- 두 번째 분수의 분자와 분모를 입력받는다. C, D = map(int, sys.stdin.readline().split())
- 두 분수의 합의 분자를 계산한다. X = A * D + B * C
- 두 분수의 합의 분모를 계산한다. Y = B * D
- 분자와 분모를 기약분수로 만들기 위해 최대공약수를 구하는 함수를 생성한다. def gcd(m, n)
- 만약 더 작은 수가 0이면 그대로 큰 수를 반환하며 종료한다. if (n == 0): return m
- 그게 아니면 두 수를 나눈 나머지를 구한다. mod = m % n
- 만약 나머지가 0이 아니면 나눠지는 수를 나눈 수로, 나누는 수를 나머지로 바꾼다. if (mod != 0): m, n = n, mod
- 바꿔진 수로 다시 최소 공배수를 찾는다. return gcd(m, n)
- 반면에 나머지가 0이면 나누는 수인 작은 수를 반환한다. else: return n
- 분자와 분모를 비교하여 큰 수, 작은 수 순서대로 함수에 대입해 최대공약수를 구한다. MAX = gcd(X, Y) if (X > Y) else gcd(Y, X)
- 각 분자와 분모를 최대공약수로 나눈다. X //= MAX Y //= MAX
- 분자와 분모를 출력한다. print(X, Y)
반응형
3. 소스코드
import sys
A, B = map(int, sys.stdin.readline().split())
C, D = map(int, sys.stdin.readline().split())
X = A * D + B * C
Y = B * D
def gcd(m, n):
if (n == 0):
return m
mod = m % n
if (mod != 0):
m, n = n, mod
return gcd(m, n)
else:
return n
MAX = gcd(X, Y) if (X > Y) else gcd(Y, X)
X //= MAX
Y //= MAX
print(X, Y)728x90
반응형
'백준' 카테고리의 다른 글
| [백준] 13909번 : 창문 닫기 - 파이썬(Python) - 우당탕탕 개발자 되기 프로젝트 (0) | 2023.11.30 |
|---|---|
| [백준] 17103번 : 골드바흐 파티션 - 파이썬(Python) - 우당탕탕 개발자 되기 프로젝트 (0) | 2023.11.29 |
| [백준] 4134번 : 다음 소수 - 파이썬(Python) - 우당탕탕 개발자 되기 프로젝트 (0) | 2023.11.28 |
| [백준] 2485번 : 가로수 - 파이썬(Python) - 우당탕탕 개발자 되기 프로젝트 (0) | 2023.11.27 |
| [백준] 13241번 : 최소공배수 - 파이썬(Python) - 우당탕탕 개발자 되기 프로젝트 (0) | 2023.11.25 |
| [백준] 11478번 : 서로 다른 부분 문자열의 개수 - 파이썬(Python) - 우당탕탕 개발자 되기 프로젝트 (0) | 2023.11.24 |
| [백준] 1269번 : 대칭 차집합 - 파이썬(Python) - 우당탕탕 개발자 되기 프로젝트 (0) | 2023.11.23 |
| [백준] 1764번 : 듣보잡 - 파이썬(Python) - 우당탕탕 개발자 되기 프로젝트 (0) | 2023.11.22 |



